Central force motion

Central force motion#

When the forces acting on an object always act some center point, you can use the conservation of angular momentum to relate radius, \(r\), and angular velocity, \(\dot{\theta}\) as such

  • \(\sum M_O = \frac{d}{dt}\left[r\hat{e}_r \times m(\dot{r}\hat{e}_r + r\dot{\theta}\hat{e}_\theta)\right]\)

  • \(0 = \frac{d}{dt}\left[mr^2\dot{\theta}\right]\hat{k}\)

  • \(mr^2\dot{\theta} = constant\)

Consider the motion of ball on a frictionless table attached to a spring in Prob 4.13,

central force notes part I:

Kinematics in cylindrical coordinates#

It helps to see the motion to understand what’s going on, the position of the ball is

\(\mathbf{r} = x\hat{i} + y\hat{j} = r(\cos\theta\hat{i} + \sin\theta \hat{j})\)

while its velocity and acceleration are represented in cylindrical coordinates

  • \(\mathbf{v} = \dot{x}\hat{i} + \dot{y}\hat{j} = \dot{r}\hat{e}_r + r\dot{\theta}\hat{e}_\theta\)

  • \(\mathbf{a} = \ddot{x}\hat{i} + \ddot{y}\hat{j} = (\ddot{r}- r\dot{\theta}^2)\hat{e}_r + (r\ddot{\theta}+2\dot{r}\dot{\theta})\hat{e}_\theta\)

Kinetics of central spring force#

The free body diagram has a single central spring force and the kinetic diagram include radial \(a_r\) and transverse \(a_\theta\) acceleration components, but no moment is applied

  1. \(\sum F_r = -k(r-L_0) = m(\ddot{r} - r\dot{\theta}^2)\)

  2. \(\sum F_\theta = 0 = m(r\ddot{\theta} + 2\dot{r}\dot{\theta})\)

  3. \(\sum M_O = 0 = \frac{d}{dt}\left(mr^2\dot{\theta}\right)\)

Equation of motion for central spring force#

Combining equations 1&3, you have a single, second order differential equation that describes radius as a function of time, \(r(t)\)

\(\ddot{r} = -\frac{k}{m}(r- L_0) + \frac{r_0^4\dot{\theta}_0^2}{r^3}\)

where \(r_0\) is the initial radius and \(\dot{\theta}_0\) is the initial angular velocity.

Initial conditions due to Impulse#

When an impulse, \(F\Delta t\), is applied to a dynamic system, you have an instantaneous change in momentum

\(F\Delta t = \Delta mv\).

It also creates a moment to create the initial angular momentum

\(M\Delta t = \Delta \mathbf{h}_O(t=0)\)

The impulse is gone after that initial impact. It gives you the initial conditions of velocity and angular momentum,

  • \(\mathbf{v}(t=0) = v_0\left(\sin45^o\hat{i} + \cos45^o\hat{j}\right) = \dot{r}\hat{e}_r + r\dot{\theta}\hat{e}_\theta\)

  • \(\mathbf{h}_O(t=0) = mL_0v_0\cos45^o = mr_0^2\dot{\theta}_0\)

Total solution and animation#

Now, you have

  1. equation of motion in terms of \(r~and~\ddot{r}\)

  2. initial conditions, \(r(t=0)=L_0~and~\dot{r}(t=0) = \frac{v_O}{\sqrt{2}}\)

So you can create a differential equation and integrate using the solve_ivp

import numpy as np
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
from scipy.integrate import solve_ivp

Here, you set up constants

  • spring constant k in N/m

  • unstretched spring length L0 in m

  • mass of ball m in kg

  • initial speed v0 in m/s note: the direction is at a 45\(^o\) angle

and define the differential equation in 2 steps:

  1. dr[0] = r[1] states \(dr/dt = \dot{r}\)

  2. dr[1] = -k/m*(r[0] - L0) +r[0]*(L0*v0/r[0])**2/2 gives the equation of motion solved for \(\ddot{r}\)

k = 100
L0 = 0.5
m = 0.5
v0 = 5

def my_ode(t, r):
    dr = np.zeros(len(r))
    dr[0] = r[1]
    dr[1] = -k/m*(r[0] - L0) +r[0]*(L0*v0/r[0])**2/2
    return dr

Integrate the equation of motion by using

  • timespan 0 to tend

  • initial conditions \(r(t=0) = L_0~and~\dot{r}(t=0) = \frac{v_0}{\sqrt{2}}\) as [L0, v0/2**0.5]

  • sol = solve_ivp integrates the equation of motion

the output for sol includes

  • timesteps sol.t

  • radius, \(r(t)\) sol.y[0]

  • radial velocity, \(\dot{r}(t)\) sol.y[1]

tend = 3
r0 = np.array([L0, v0/2**0.5])
sol = solve_ivp(my_ode, [0, tend], r0, t_eval = np.linspace(0, tend, 500))
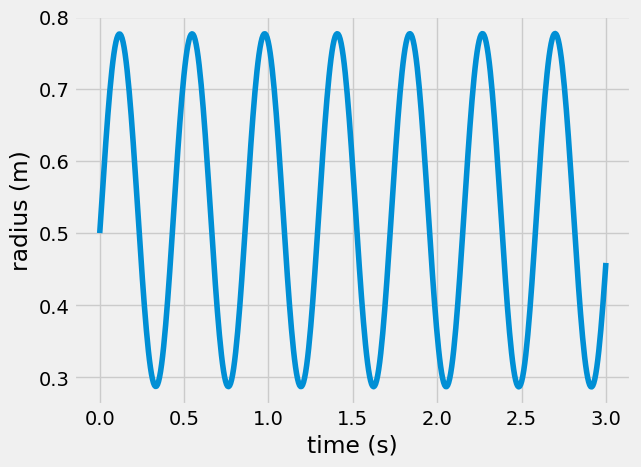
plt.plot(sol.t, sol.y[0])
plt.xlabel('time (s)')
plt.ylabel('radius (m)')

Text(0, 0.5, 'radius (m)')
../_images/a4b265464495d5fb768e0a445aabc5215bcd71c8ac3b697299546fb31a9b7b96.png

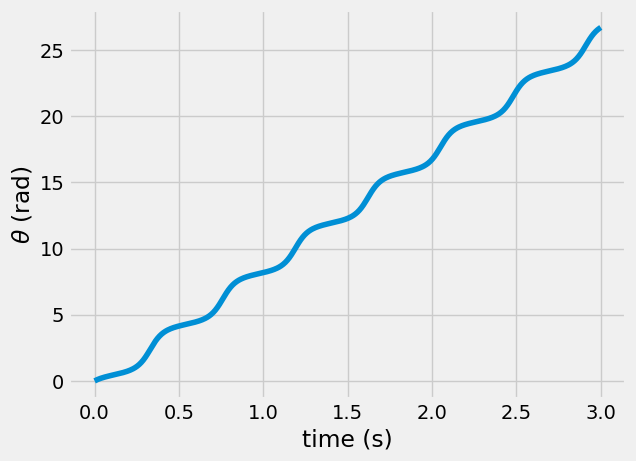
You don’t have an equation for \(\theta(t)\), but you can use angular momentum to calculate \(\dot{\theta}\)

\(\dot{\theta}(t) = \frac{h_O(t=0)}{r^2}\)

then, the solution for \(\theta = \sum\dot{\theta}dt\) or np.cumsum(dtheta*sol.t[1]) - theta[0]

dtheta = L0*v0/2**0.5/sol.y[0]**2
theta = np.cumsum(dtheta*sol.t[1])
theta += -theta[0]
plt.plot(sol.t, theta)
plt.xlabel('time (s)')
plt.ylabel(r'$\theta$ (rad)')

Text(0, 0.5, '$\\theta$ (rad)')
../_images/5bd0af85e08307626b3af426fb17fa27c72f5c95d1e0646a9c02bcfbcddbc7d5.png

Finally, you can get the \(r-\theta\) coordinates back into \(x-y\) coordinates and animate the motion

x = sol.y[0]*np.cos(theta)
y = sol.y[0]*np.sin(theta)
Hide code cell content 
from matplotlib import animation
from IPython.display import HTML

fig, ax = plt.subplots()

#ax.set_xlim(( -30, 30))
# ax.set_ylim((1.5, -1.5))
ax.axis('equal')
ax.set_xlabel('x-position (m)')
ax.set_ylabel('y-position (m)')

line1, = ax.plot([], [],'-o')
line2, = ax.plot(x, y,'g--', alpha=0.5)

def init():
    line1.set_data([], [])
    line2.set_data([], [])
    return (line1, line2, )

def animate(i):
    '''function that updates the line and marker data
    arguments:
    ----------
    i: index of timestep
    outputs:
    --------
    line: the line object plotted in the above ax.plot(...)
    '''
    line1.set_data([0, x[i]], [0, y[i]])
    line2.set_data(x[0:i], y[0:i])
    return (line1, line2, )

anim = animation.FuncAnimation(fig, animate, init_func=init,
                               frames=range(0,len(sol.t)), interval=50, 
                               blit=True)
../_images/4daa63ee75e0c138051bbc10398c190aed9f18950b5e7a73e4b69b423c19adfd.png 
HTML(anim.to_html5_video())

---------------------------------------------------------------------------
RuntimeError                              Traceback (most recent call last)
Cell In[7], line 1
----> 1 HTML(anim.to_html5_video())

File /opt/hostedtoolcache/Python/3.9.21/x64/lib/python3.9/site-packages/matplotlib/animation.py:1265, in Animation.to_html5_video(self, embed_limit)
   1262 path = Path(tmpdir, "temp.m4v")
   1263 # We create a writer manually so that we can get the
   1264 # appropriate size for the tag
-> 1265 Writer = writers[mpl.rcParams['animation.writer']]
   1266 writer = Writer(codec='h264',
   1267                 bitrate=mpl.rcParams['animation.bitrate'],
   1268                 fps=1000. / self._interval)
   1269 self.save(str(path), writer=writer)

File /opt/hostedtoolcache/Python/3.9.21/x64/lib/python3.9/site-packages/matplotlib/animation.py:128, in MovieWriterRegistry.__getitem__(self, name)
    126 if self.is_available(name):
    127     return self._registered[name]
--> 128 raise RuntimeError(f"Requested MovieWriter ({name}) not available")

RuntimeError: Requested MovieWriter (ffmpeg) not available

Wrapping up#

In this notebook, you used conservation of angular momentum and Newton’s second law to create an equation of motion for the radius of a spring-mass stationary table. Then, you plotted the results and watched the path of the object over time.

Next steps:

  • What happens if you change the parameters of the system, \(k,~L0,~etc.\)?

  • What happens if you change the initial impulse applied to the ball?

Contents