Show code cell content
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
from IPython.core.display import SVG
Mechanical advantage#
In the diagram below, there is a 50-N force, \(F\), applied downwards on a constrained linkage system. There is a restoring force, \(R\), that maintains a slow change in the angle of the mechanism, \(\theta\), as it changes from \(89^o\) to \(-89^o\). Your goal is to determine the necessary restoring force \(R\) as a function of angle \(\theta\).
Kinematics - geometry of motion#
This system has two rigid bodies connected at point \(A\) by a pin and the whole system is pinned to the ground at \(O\). Point \(B\) slides along a horizontal surface. The total degrees of freedom are
3 (link 1) + 3 (link 2) - 2 constraints (\(O\)) - 2 constraints (\(A\)) - 1 constraint (\(B\)) - 1 constraint (\(\theta\)-fixed) = 0 DOF
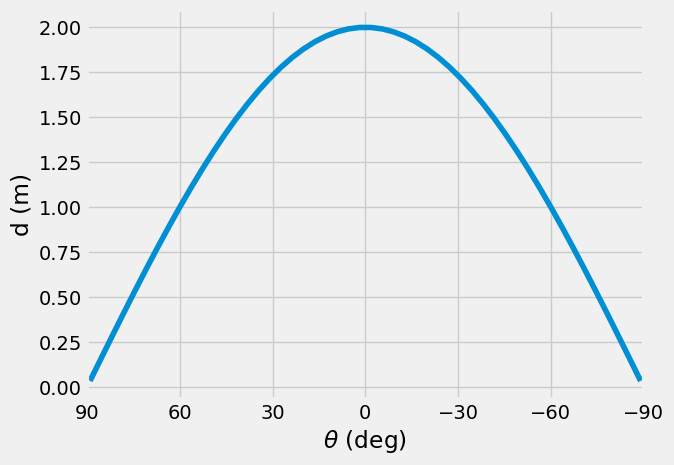
For a given angle \(\theta\), there can only be one configuration in the system. Create the constraint equations using the relative position of point \(A\) as such
\(\mathbf{r}_A = \mathbf{r}_{A/B} + \mathbf{r}_B\)
where
\(\mathbf{r}_A = L(\cos\theta \hat{i}+ \sin\theta \hat{j})\)
\(\mathbf{r}_B = d\hat{i}\)
\(\mathbf{r}_{A/B} = L(-\cos\theta \hat{i} + \sin\theta \hat{j})\)
solving for the \(\hat{i}-\) and \(\hat{j}-\)components creates two equations that describe the state of the system
\(\theta = \theta\) which states because we have an isosceles triangle, two angles have to be equal
\(d = 2 L \cos\theta\) so \(\mathbf{r}_{B} = 2L \cos\theta \hat{i}\)
Show code cell source
theta = np.linspace(89,-89)*np.pi/180
d = 2*1*np.cos(theta)
plt.plot(theta*180/np.pi, d)
plt.xticks(np.arange(-90,91,30))
plt.xlabel(r'$\theta$ (deg)')
plt.xlim(90,-90)
plt.ylabel('d (m)');
Kinetics - applied forces and constraint forces#
The applied force, \(F=50~N\) is constant, but \(R\) is dependent upon the geometry of the system. You solved for the kinematics in the first part, here you can use the Newton-Euler equations to solve for \(R\) given \(\theta\) and \(F\). Separate the system into the left and right links,
The Newton-Euler equations:
\(\mathbf{F} = m\mathbf{a} = \mathbf{0}\) links moving slowly
\(M_G = I\alpha = 0\) links rotating slowly
Newton-Euler equations for the left bar:
\(\mathbf{F}\cdot \hat{i} = N_{x1}+N_{x2} = 0\)
\(\mathbf{F}\cdot \hat{i} = N_{y1}+N_{y2} - F = 0\)
\(M_O = l\hat{b}_1 \times (-F\hat{j} + N_{x2}\hat{i} + N_{y2}\hat{j}) = 0\)
Newton-Euler equations for the right bar:
\(\mathbf{F}\cdot \hat{i} = -N_{x2}-R = 0\)
\(\mathbf{F}\cdot \hat{i} = -N_{y2}+N_{y3} = 0\)
\(M_A = l\hat{c}_1 \times (-R\hat{i} + N_{y3}\hat{j})= 0\)
Note: Don’t count \(F\) twice! You can use the applied force on the left or right, but not both. Try solving the equations placing it on the right bar.
The four equations for \(\mathbf{F}\) relate the reaction forces \(\mathbf{N}_{1},~\mathbf{N}_{2},~and~\mathbf{N}_{3}\). The two moment equations relate \(R\) to \(F\) and \(\theta\) as such
\(N_{y2}L\cos\theta - RL\sin\theta = 0\)
and
\(-FL\cos\theta +N_{y2}\cos\theta+RL\sin\theta = 0\)
combining there results
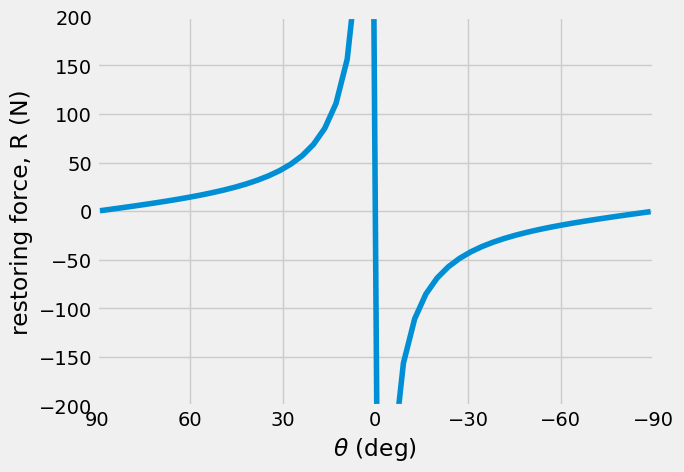
\(F\cos\theta = 2R\sin\theta\rightarrow R = \frac{F}{2}\cot\theta\)
Show code cell source
R = 50/2*np.tan(theta)**-1
plt.plot(theta*180/np.pi, R)
plt.xticks(np.arange(-90,91,30))
plt.xlabel(r'$\theta$ (deg)')
plt.ylabel('restoring force, R (N)')
plt.xlim(90,-90)
plt.ylim(-200,200);
Wrapping up#
Take a look at the mechanical advantage and disadvantage this system can create. For angles close to \(\theta\approx 90^o\), the restoring force is close to zero. In this case, the applied force is mostly directed at constraints on the system. When the angles are close to \(\theta \approx 0^o\), the required restoring force can be \(>100\times\) the input force.
Have you seen this type of linkage system in engineering devices?