Rigid body motion

Rigid body motion#

Describing the motion of a single point requires some description of its position in 3D space. Some examples that we commonly use are Cartesian coordinates,

\(\mathbf{r} = x\hat{i} + y\hat{j} + z\hat{k}\)

where x, y, and z are independent measures of distance from our chosen origin.

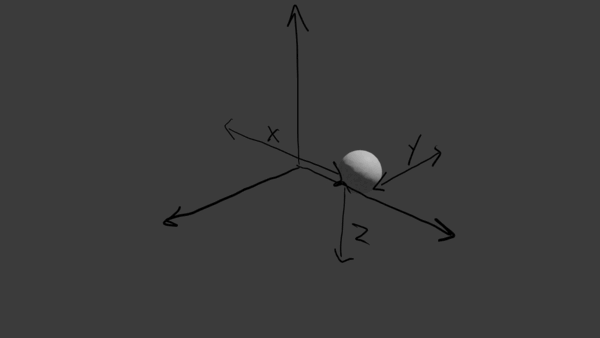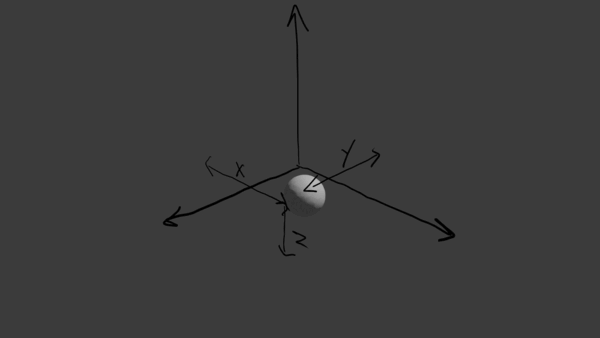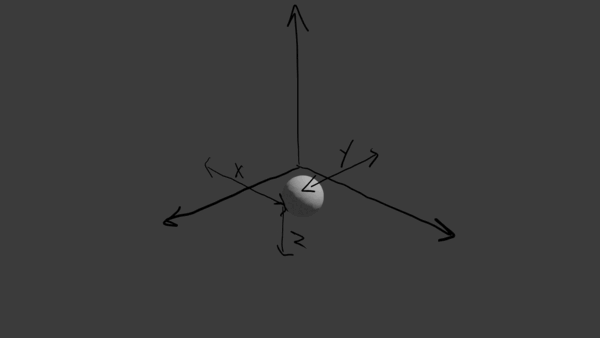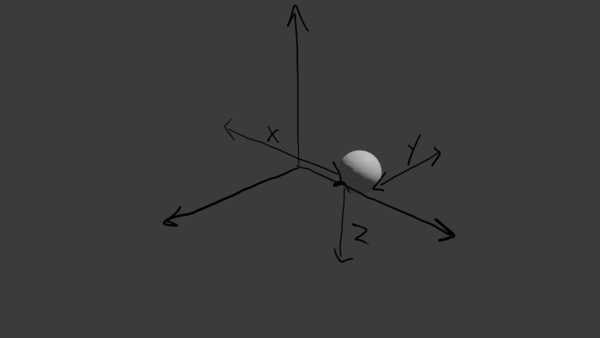
Tracking the position of a point in 3D space using x, y, and zcoordindates

Describing the motion of a rigid body, like an airplane, could be done by describing all of the points that make up the airplane. This would mean we need to split the airplane into lots of points and keep track of each one individually. This would quickly turn into a difficult problem depending on how many points we decide to describe e.g. maybe we create a description of all 33 octillion Aluminum atoms in a 1500-kg airplane.

Degrees of Freedom#

If we consider an airplane as a rigid object (ignoring the elastic stretching and bending that is relatively small), then we can start to reduce its degrees of freedom to a reasonable number of measureable quantities.

The degrees of freedom are the minimum number of independent quantities needed to describe the position of an object or system.

We could choose to describe the airplane’s position using its center of mass. Now, if the airplane has a latitude, longitude, and altitude we know exactly where it is. But, how do we keep track of where the rest of the plane is? Is the nose higher than the tail (take-off)? Is the plane facing North? South? We need more quantities to describe the position and orientation of the airplane. In this case, we can use the pitch, roll, and yaw

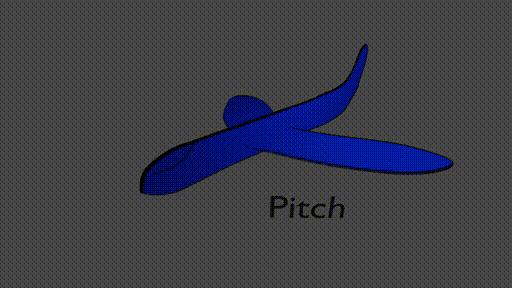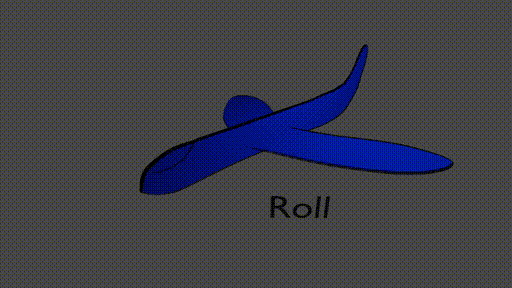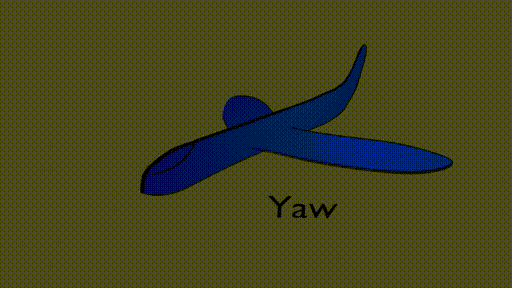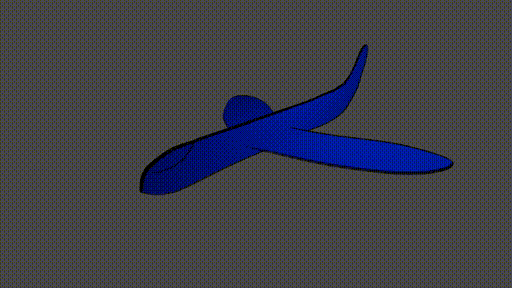
Tracking the pitch, roll, and yaw of anairplane

Now, we have 6 degrees of freedom that describe the position of the airplane,

  • x, y, z - positions

  • pitch, roll, and yaw - orientations

This is a much more manageable set of numbers to report and describe than the positions of each atom.

Constraints on motion#

When we need to describe the position of an object moving in one plane (not airplane, but instead the x-y-plane) there are less degrees of freedom because we don’t need to keep track of one of the z-position, and all of the rotation happens along the z-axis. So the degrees of freedom become

  • x, y - positions

  • pitch, \(\theta\)

We created 3 constraints on the object,

  1. z = constant

  2. roll = constant

  3. yaw = constant

Constraints on a system or object reduce the degrees of freedom as such DOF = total degrees of freedom - number of constraints

Contents