Homework #7 Kinematics
Contents
import numpy as np
from numpy import sin,cos,pi
from scipy.linalg import *
from scipy.optimize import fsolve,root
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
from IPython.display import YouTubeVideo
YouTubeVideo('-A1w46iqUlE')
Homework #7 Kinematics¶
Kinematics is the study of the geometry of motion e.g. definitions of position, velocity, and acceleration
In this notebook we will explore kinematically-driven systems where the system degrees of freedom, \(n_{d}=0 = 3\times n_b -n_c\), for planar problems. \(n_b\) bodies moving in a plane have \(3\times n_b\) degrees of freedom and the number of constraints is \(n_c\).
 https://learning.oreilly.com/api/v2/epubs/urn:orm:book:9780470686157/files/figs/0303.png
https://learning.oreilly.com/api/v2/epubs/urn:orm:book:9780470686157/files/figs/0303.png
In the figure above, there are three position vectors, \(\mathbf{r}^{i}\), \(\mathbf{R}^{i}\), and \(\mathbf{u}^{i}\) and two coordinate systems, \(X\)-\(Y\) and \(X^{i}\)-\(Y^{i}\).
The \(X^{i}\)-\(Y^{i}\) coordinate system moves with the rigid body and the point P is always in a fixed position \(\mathbf{\bar{u}}^{i}_{P}=\bar{x}^{i}_{P}\hat{i}^{i}+\bar{y}^{i}_{P}\hat{j}^{i}\) in this coordinate system.
\(\mathbf{u}^{i}_{P} = \left[ \begin{array}{cc} \cos \theta^i & -\sin \theta^i \\ \sin \theta^i & \cos \theta^i \\ \end{array} \right] \left[\begin{array}{c} \bar{x}^{i}_{P} \\ \bar{y}^{i}_{P}\end{array}\right]\)
or
\(\mathbf{u}_{P}^{i}=\mathbf{A}^{i}\mathbf{\bar{u}}^{i}_{P}\)
def rotA(theta):
'''This function returns a 2x2 rotation matrix to convert the
rotated coordinate to the global coordinate system
input is angle in radians
Parameters
----------
theta : angle in radians
Returns
-------
A : 2x2 array to rotate a coordinate system at angle theta to global x-y
'''
A=np.zeros((2,2))
A=np.array([[np.cos(theta), -np.sin(theta)],
[np.sin(theta), np.cos(theta)]])
return A
rotA(np.pi/3)
array([[ 0.5 , -0.8660254],
[ 0.8660254, 0.5 ]])
Figs. Slider crank mechanism and body coordinate systems.
Computational Kinematics of Slider crank¶
Here you will create the computational kinematics of the slider crank in Fig. 3.35-3.36 above.
The first kinematic problem will drive the slider crank with a constraint $\(\theta^{1} = \omega t +\theta_0\)$
where \(\omega = 150~rad/s\) and \(\theta_0=\pi/6~rad\).
Below you set up the function to return the constraint equations,
\(\mathbf{C}(\mathbf{q},t)\) = C_slidercrank(q,t)
def links(l1 = 0.075*2, l2 = 0.175*2):
'''function to define lengths of links for bodies 2 and 3
in Fig. 3.35-3.36
Parameters
----------
l1 : length of body one, default 0.150 m
l2 : lenght of body two, default 0.250 m
Returns
-------
l1, l2 : link lengths for bodies 1 and 2
'''
return l1,l2
def C_slidercrank(q,t):
'''9 constraint equations for 9 generalized coords
q=[R1x,R1y,a1,R2x,R2y,a2,R3x,R3y,a3]
q=[R1, a1, R2, ,a2, R3, ,a3]
[0,1 2 3,4 5 6,7 8 ]
1/\2
/ \ slider-crank mechanism
O |3|
^^^-------------
Parameters
----------
q : numpy array for 9 generalized coordinates for bodies 1-3 in the slider crank
q = [q1, q2, q3]
t : current time
Returns
-------
C : 9 constraint equation evaluations
'''
l1,l2=links()
q1 = q[0:3]
q2 = q[3:6]
q3 = q[6:9]
C=np.zeros(9)
C[0:2] = q1[0:2]+rotA(q1[2])@np.array([-l1/2, 0])
C[2:4] = q1[0:2]-q2[0:2]+rotA(q1[2])@np.array([l1/2, 0])-rotA(q2[2])@np.array([-l2/2, 0])
C[4:6] = q2[0:2]-q3[0:2]+rotA(q2[2])@np.array([l2/2, 0])-rotA(q3[2])@np.array([0, 0])
C[6] = q3[1]
C[7] = q3[2]
C[8] = q1[2] - pi/6 - 150*t
return C
Problem 1¶
Solve for \(\mathbf{q}(t=0) = [R_x^1,~R_y^1, \theta^1,~R_x^2,~R_y^2, \theta^2,~R_x^3,~R_y^3, \theta^3]\) using the given system definitions:
\(l_1 = 0.15~m\)
\(l_2 = 0.25~m\)
\(\theta^1(t) = 150t+\frac{\pi}{6}\)
Show that C_slidercrank(q0, 0) \(=\mathbf{0}\).
## your work here
Set up solution for \(\mathbf{C}(\mathbf{q},~t)\)¶
Next, set up the \(9\times 9\) Jacobian of
Set up the \(\mathbf{A}_\theta\) function as
A_thetaeach pin \(\mathbf{C_{q,~pin}}=\frac{\partial\mathbf{C_{pin}}}{\partial\mathbf{q}}\)=
Cq_pinthe total system: \(\mathbf{C_{q}}=\frac{\partial\mathbf{C}}{\partial\mathbf{q}}\)=
Cq_slidercrank
def A_theta(theta):
'''This function returns a 2x2 rotation matrix derivative
input is angle in radians
Parameters
----------
theta : angle in radians
Returns
-------
dAda : 2x2 array derivative of `rotA`
'''
dAda=np.array([[-np.sin(theta), -np.cos(theta)],
[np.cos(theta), -np.sin(theta)]])
return dAda
def Cq_pin(qi, qj, ui, uj):
'''Jacobian of a pinned constraint for planar motion
Parameters
----------
qi : generalized coordinates of the first body, i [Rxi, Ryi, thetai]
qj : generalized coordinates of the 2nd body, i [Rxj, Ryj, thetaj]
ui : position of the pin the body-i coordinate system
uj : position of the pin the body-j coordinate system
Returns
-------
Cq_pin : 2 rows x 6 columns Jacobian of pin constraint Cpin
'''
Cq_1=np.block([np.eye(2), A_theta(qi[2])@ui[:,np.newaxis] ])
Cq_2=np.block([-np.eye(2), -A_theta(qj[2])@uj[:,np.newaxis] ])
Cq_pin=np.block([Cq_1, Cq_2])
return Cq_pin
def Cq_slidercrank(q,t):
'''return Jacobian of C_slidercrank(q,t) = dC/dq_i
|dC1/dR1x dC1/dR1y ... dC9/da3 |
|dC2/dR1x dC2/dR1y ... dC9/da3 |
|... .. . ... |
| . |
| . |
|dC9/dR1x ... dC9/da3 |
Parameters
----------
q : numpy array for 9 generalized coordinates for bodies 1-3 in the slider crank
q = [q1, q2, q3]
t : current time
Returns
-------
Cq : 9 rows x 9 columns Jacobian of constraints `C_slidercrank`
'''
l1, l2 = links()
q1 = q[0:3]
q2 = q[3:6]
q3 = q[6:9]
Cq=np.zeros((9,9))
Cq[0:2, 0:3] = Cq_pin(q1, np.array([0, 0, 0]),np.array([-l1/2, 0]),np.array([0, 0]))[0:2, 0:3]
Cq[2:4, 0:6] = Cq_pin(q1, q2, np.array([l1/2, 0]), np.array([-l2/2, 0]))
Cq[4:6, 3:10] = Cq_pin(q2, q3, np.array([l2/2, 0]), np.array([0, 0]))
Cq[6:8, 7:10] = np.eye(2)
Cq[8, 2]=1
return Cq
Solve for \(\mathbf{q(t)}\)¶
Now, you solve for 1 full rotation of the driven crank.
t= 0-360\(^o\) = 0-2\(\pi\)/150
The solution requires an initial guess for the generalized coordinates, \(\mathbf{q}\), set as q0. It is updated at each timestep to find the next solution. Here, you use the Jacobian of \(\mathbf{C}\), \(\mathbf{C_q}\), by specifying the fprime = lambda q: Cq_slidercrank.
t = np.linspace(0, 2*pi/150)
q0 = np.array([0, 0.5, pi/6, 0, 0.5, pi/3, 0.5, 0, 0])
q = np.zeros((len(q0), len(t)))
q[:, 0] = q0
for i,tt in enumerate(t):
q[:,i]=fsolve(lambda q: C_slidercrank(q,tt),q0,\
fprime= lambda q: Cq_slidercrank(q,tt)) # <-- use the Jacobian to speed up solution
q0=q[:,i]
Now, you can create the same figures as Shabana ch 3

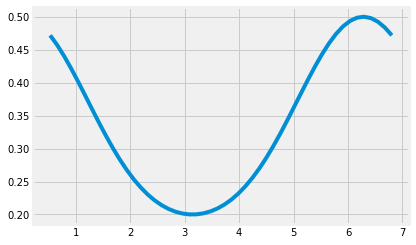
Fig. 3.37. Orientation of the connecting rod

Fig. 3.37. Displacement of the slider block
plt.plot(q[2,:],q[6,:])
#plt.plot(t,q[5,:]/pi*180)
[<matplotlib.lines.Line2D at 0x70099bbd0670>]
Problem 2¶
Recreate the displacement of the slider block graph in Fig. 3.38 from your solution.
## your work here
Animate the motion for constant \(\dot{\theta}^1\)¶
Next, you animate the motion of the system. Below, you create
plot_shapeto create lines and markers to represent links and the sliding basea figure that shows the path of the two link centers of mass 3.
initto initialize the animationanimateto update the two links and sliding baseFuncAnimationto display the motion of the slidercrank system
def plot_shape(shape,dims,q):
'''
function to plot a shape based upon the shape dimensions and coordinates
arguments:
----------
shape: either 'link' or 'base',
- the link returns two points to plot as a line
- the base returns one point to plot as a marker
- if neither 'link' or 'base' are chosen, then 0 is returned and warning printed
`choose a \'link\' or \'base\' please`
dims: the dimensions of the shape
- the link uses the first value as the length
- the base ignores the `dims`
q: generalized coordinates in the form [Rx, Ry, theta]
- the link returns the center of the link at (Rx, Ry) and oriented at theta
- the base returns the center at (Rx, Ry) and ignores theta
returns:
--------
datax: coordinates to plot the x-positions
datay: coordinates to plot the y-positions
- the link returns array of length 2
- the base returns array of length 1
'''
if shape=='link':
left = rotA(q[2])@np.array([-dims[0]/2, 0])
right = rotA(q[2])@np.array([dims[0]/2, 0])
Px=q[0]+np.array([left[0], right[0]])
Py=q[1]+np.array([left[1], right[1]])
datax = Px
datay = Py
#l,= plt.plot(Px,Py,'o-')
return datax, datay
elif shape=='base':
Px=q[0]
Py=q[1]
data = [Px, Py]
#l,=plt.plot(Px,Py,'s',markersize=20)
return data
else:
print('choose a \'link\' or \'base\' please')
return 0
2. initialize the lines and coordinate system¶
q1 = q[0:3, :]
q2 = q[3:6, :]
q3 = q[6:9, :]
l1, l2 = links()
fig, ax = plt.subplots()
link1, = ax.plot([], [], linewidth = 10)
link2, = ax.plot([], [], linewidth = 10)
body3, = ax.plot([], [], 's', markersize = 20)
path1, = ax.plot(q1[0, :], q1[1, :])
path2, = ax.plot(q2[0, :], q2[1, :])
ax.set_xlim((-0.25, 0.5))
ax.set_ylim((-0.25, 0.25))
ax.set_xlabel('X-axis (m)')
ax.set_ylabel('Y-axis (m)')
ax.set_title('Slider crank motion and paths')
Text(0.5, 1.0, 'Slider crank motion and paths')
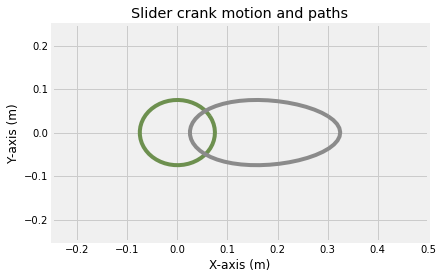
3. and 4. create your init and animation functions to update the lines on the plot¶
Create an initializing (init) function that clears the previous lines and markers
Create an animating (animate) function that updates the link, base, and path
def init():
link1.set_data([], [])
link2.set_data([], [])
body3.set_data([], [])
return (link1, link2, body3)
def animate(i):
'''function that updates the line and marker data
arguments:
----------
i: index of timestep
outputs:
--------
link1: the line object plotted in the above ax.plot(...)
link2: the line object plotted in the above ax.plot(...)
body3: the marker for the piston in the slider-crank
'''
l1, l2 = links()
datax, datay = plot_shape('link', np.array([l1]), q1[:, i])
link1.set_data(datax, datay)
datax, datay = plot_shape('link', np.array([l2]), q2[:, i])
link2.set_data(datax, datay)
pinx, piny = plot_shape('base', [], q3[:,i])
body3.set_data(pinx, piny)
return (link1, link2, body3, )
4. display the result in an HTML video¶
Import the animation and HTML functions. Then, create an animation (anim) variable using the animation.FuncAnimation
from matplotlib import animation
from IPython.display import HTML
anim = animation.FuncAnimation(fig, animate, init_func=init,
frames=range(0,len(t)), interval=50,
blit=True)
HTML(anim.to_html5_video())
Velocity and Acceleration¶
Differentiating the constraint equations, \(\mathbf{Cq}=\mathbf{0}\),
\(\mathbf{C_q \dot{q}}+\mathbf{C}_t=\mathbf{0}\) (3.119)
where
\(\mathbf{C}_t = \left[\frac{\partial C_1}{\partial t} \frac{\partial C_2}{\partial t} ... \frac{\partial C_n}{\partial t}\right]^T\) (3.120)
Solve for velocity \(\mathbf{\dot{q}_i}\) as such
\(\mathbf{C_q \dot{q}}=-\mathbf{C}_t\) (3.121)
Differentiating \(\mathbf{Cq}=\mathbf{0}\) twice leads to the acceleration equation
\(\mathbf{C_q \ddot{q}}+ \left(\mathbf{C_q \dot{q}}\right)_{\mathbf{q}}\mathbf{\dot{q}}+ 2\mathbf{C}_{\mathbf{q}t}\mathbf{\dot{q}}+ \mathbf{C}_{tt}=\mathbf{0}\) (3.123)
Solve for acceleration \(\mathbf{\ddot{q}}\) as such
\(\mathbf{C_q \ddot{q}}=\mathbf{Q}_d\)
where
\(\mathbf{Q}_d=-\left(\mathbf{C_q \dot{q}}\right)_{\mathbf{q}}\mathbf{\dot{q}}- 2\mathbf{C}_{\mathbf{q}t}\mathbf{\dot{q}}- \mathbf{C}_{tt}\)
For the current slider crank system,
\(\mathbf{Q}_d= \left[\begin{array} ~(\dot{\theta}^1)^2\mathbf{A}^1\mathbf{\bar{u}}^{1}_{A}\\ (\dot{\theta}^1)^2\mathbf{A}^1\mathbf{\bar{u}}^{1}_{B}-(\dot{\theta}^2)^2\mathbf{A}^2\mathbf{\bar{u}}^{2}_{B}\\ (\dot{\theta}^2)^2\mathbf{A}^2\mathbf{\bar{u}}^{i}_{C}\\ 0\\ 0\\ 0\end{array}\right]\)
Here, you set up vel_acc(q,t) to return velocity and acceleration of \(\mathbf{q_{i}}\) components as \(\frac{d\mathbf{q}}{dt}\) and \(\frac{d^2\mathbf{q}}{dt^2}\) (dq and ddq, respectively)
def Qd_slidercrank(q, dq, t):
'''return slidercrank Qd = Cq@ddq
Parameters
----------
q : numpy array for 9 generalized coordinates for bodies 1-3 in the slider crank
q = [q1, q2, q3]
t : current time
Returns
-------
Qd : 1D array with length 9
'''
l1, l2 = links()
q1 = q[0:3]
q2 = q[3:6]
q3 = q[6:9]
dq1 = dq[0:3]
dq2 = dq[3:6]
dq3 = dq[6:9]
Qd=np.zeros(9)
Qd[0:2] = dq1[2]**2*rotA(q1[2])@np.array([-l1/2, 0])
Qd[2:4] = dq1[2]**2*rotA(q1[2])@np.array([l1/2, 0]) -\
dq2[2]**2*rotA(q2[2])@np.array([-l2/2, 0])
Qd[4:6] = dq2[2]**2*rotA(q2[2])@np.array([l2/2, 0])
Qd[6:9] = 0
return Qd
def Ct_slidercrank(q, t):
'''return slidercrank partial derivative of constraints dC/dt
Parameters
----------
q : numpy array for 9 generalized coordinates for bodies 1-3 in the slider crank
q = [q1, q2, q3]
t : current time
Returns
-------
Ct : 1D array with length 9
'''
Ct = np.zeros(9)
Ct[8] = -150
return Ct
t = np.linspace(0, 2*pi/150)
q0 = np.array([0, 0.5, pi/6, 0, 0.5, pi/3, 0.5, 0, 0])
q = np.zeros((len(q0), len(t)))
dq = np.zeros(q.shape)
ddq = np.zeros(q.shape)
q[:, 0] = q0
for i, ti in enumerate(t):
q[:, i] = fsolve(lambda q: C_slidercrank(q, ti),q0,\
fprime= lambda q: Cq_slidercrank(q, ti)) # <-- use the Jacobian to speed up solution
dq[:, i] = np.linalg.solve(Cq_slidercrank(q[:,i], ti), -Ct_slidercrank(q[:, i], ti))
Qd = Qd_slidercrank(q[:, i], dq[:, i], ti)
ddq[:, i] = np.linalg.solve(Cq_slidercrank(q[:,i], ti), Qd)
q0=q[:, i]


Fig. 3.38 velocity components


Fig. 3.39 acceleration components
Recreate the plots with your solution¶
Here, you can plot the terms \(\dot{\mathbf{q}}\) and \(\ddot{\mathbf{q}}\) to compare to the Shabana solutions shown above in Figs 3.38-39. Try plotting \(\dot{\theta}^2,~\ddot{\theta}^2,~\dot{R}^3_x,~and~\ddot{R}^3_x\)
Problem 3¶
Change the constraints for the slidercrank such that
\(R^4_x-f(t)=0\)
where
\(f(t)=0.35-0.8l^2\sin150t\)
Recreate Figs. 3.43-3.48 for the slidercrank.