Project 05 - String vibrations of guitars

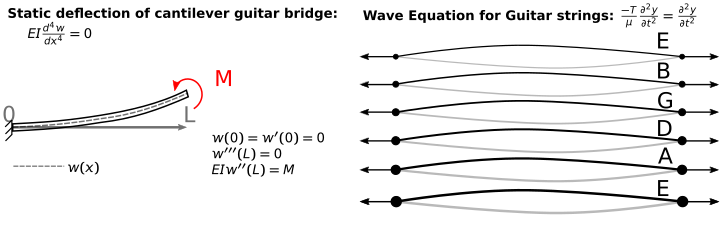
In this final project, you will consider all six strings of a guitar and the deflection of the neck of the guitar. Here are the inputs for each of the strings, all L=0.64 m:

string	density (g/m)	tension (kg)
E	0.401	7.28
B	0.708	7.22
G	1.140	7.32
D	2.333	8.41
A	4.466	9.03
E	6.790	7.71

1. The neck of the guitar can be considered a cantilever beam with an applied moment, shown above. At the tip you have a moment equal to the sum of the (tensions in the strings) \(\times\) (bridge height). Here you will consider it as \(h=4~mm\).

a. Use a finite difference approximation to determine the deflection of the guitar’s bridge if the Young’s modulus is E=10 GPa and it is a rectangular cross-section \(2\times4~cm^2\) and \(I=\frac{4\cdot2^3}{12}~cm^4.\)

b. Demonstrate that your finite difference solution has converged. e.g. decrease the step size \(h\) and show the solution converges to a final value.

import numpy as np
from scipy import linalg
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')

L = 0.64
N = 10
dx = L/(N)
I = 4*2**3/12*1/(100**4) # convert cm^4 -> m^4
E = 10e9 # N/m^2
string_vals = np.array([[0.401e-3,7.28],
                        [0.708e-3,7.22],
                        [1.14e-3,7.32],
                        [2.333e-3,8.41],
                        [4.466e-3,9.03],
                        [6.79e-3,7.71]])
M = np.sum(string_vals[:,1]*9.81)*4e-3

2. Here, record the first three frequencies of the 6-string guitar.

a. Consider the G-string on the guitar, L=0.64 m, \(\mu=1.14~g/m,\) and T=71.81 N [1].

Guitar string equation: \(\mu\frac{\partial^2 y}{\partial t^2}=T\frac{\partial ^2 y}{\partial x^2}\)

a. Calculate the first, second, and third natural frequencies using 6, 30, 45, and 60 nodes. Plot the mode shapes and determine the number of nodes needed to converge for the first three modes.

def guitar_modes(N,L = 0.64,T = 71.81,mu = 1.14e-3):
    '''General Finite Difference Wave Equation
    in a guitar string
    of the form T/mu*d^2y/dx^2=d^2y/dt^2
    Arguments:
    ----------
    N: number of elements in guitar string finite diff
    L: length of guitar string
    T: tension in string
    mu: string density in kg/m
    Returns:
    ----------
    e: eigenvalues (frequency [rad/s]) of guitar string
    v: eigenvectors (mode shapes) of guitar string
    '''
    dx = L/(N+1)

b. Use the number of nodes necessary for convergence to calculate the first 3 modes of vibration for the other 5 strings on the guitar. Display the first three natural frequencies for all six strings.

In this final project, you will consider all six strings of a guitar and the deflection of the neck of the guitar. Here are the inputs for each of the strings, all L=0.64 m:

string	density (g/m)	tension (kg)
E	0.401	7.28
B	0.708	7.22
G	1.140	7.32
D	2.333	8.41
A	4.466	9.03
E	6.790	7.71

string_name = ['E','B','G','D','A','E']
string_vals = np.array([[0.401e-3,7.28],
                        [0.708e-3,7.22],
                        [1.14e-3,7.32],
                        [2.333e-3,8.41],
                        [4.466e-3,9.03],
                        [6.79e-3,7.71]])

c. Create an audio signal that has the 18 frequencies (6 strings \(\times\) 3 modes) in an array and display it using the from IPython.display import Audio library.

Hint: you don’t need to solve the differential equations here. You can use the calculated frequencies to add sine-waves together: \(\sin(f_12\pi t)+\sin(f_22\pi t)+...\)

rate = 20000
t = np.linspace(0,3,rate*3)
signal = np.zeros(len(t))

from IPython.display import Audio

Audio(data = signal,rate=rate)

/home/ryan/miniconda3/envs/nbdev/lib/python3.10/site-packages/IPython/lib/display.py:187: RuntimeWarning: invalid value encountered in divide
  scaled = data / normalization_factor * 32767
/home/ryan/miniconda3/envs/nbdev/lib/python3.10/site-packages/IPython/lib/display.py:188: RuntimeWarning: invalid value encountered in cast
  return scaled.astype("<h").tobytes(), nchan