import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
plt.style.use('fivethirtyeight')
from numpy.random import default_rng

Project #02 - NYSE random walk predictor

In the Stats and Monte Carlo module, you created a Brownian motion model to predict the motion of particles in a fluid. The Monte Carlo model took steps in the x- and y-directions with random magnitudes.

This random walk can be used to predict stock prices. Let’s take a look at some data from the New York Stock Exchange NYSE from 2010 through 2017.

Important Note: I am not a financial advisor and these models are purely for academic exercises. If you decide to use anything in these notebooks to make financial decisions, it is at your own risk. I am not an economist/financial advisor/etc., I am just a Professor who likes to learn and exeriment.

Here, I will show an example workflow to analyze and predict the Google stock price [GOOGL] from 2010 - 2014. Then, you can choose your own stock price to evaluate and create a predictive model.

1. Explore data and select data of interest

2. Find statistical description of data: mean and standard deviation

3. Create random variables

4. Generate random walk for [GOOGL] stock opening price

1. Explore data

Here, I load the data into a Pandas dataframe to see what headings and values are available. I see two columns that I want to analyze

• ‘date’

• ‘open’

data = pd.read_csv('../data/nyse-data.csv')
data['date'] = pd.to_datetime(data['date'], format='ISO8601')
data

	date	symbol	open	close	low	high	volume
0	2016-01-05	WLTW	123.430000	125.839996	122.309998	126.250000	2163600.0
1	2016-01-06	WLTW	125.239998	119.980003	119.940002	125.540001	2386400.0
2	2016-01-07	WLTW	116.379997	114.949997	114.930000	119.739998	2489500.0
3	2016-01-08	WLTW	115.480003	116.620003	113.500000	117.440002	2006300.0
4	2016-01-11	WLTW	117.010002	114.970001	114.089996	117.330002	1408600.0
...	...	...	...	...	...	...	...
851259	2016-12-30	ZBH	103.309998	103.199997	102.849998	103.930000	973800.0
851260	2016-12-30	ZION	43.070000	43.040001	42.689999	43.310001	1938100.0
851261	2016-12-30	ZTS	53.639999	53.529999	53.270000	53.740002	1701200.0
851262	2016-12-30	AIV	44.730000	45.450001	44.410000	45.590000	1380900.0
851263	2016-12-30	FTV	54.200001	53.630001	53.389999	54.480000	705100.0

851264 rows × 7 columns

I only want the symbol == GOOGL data, so I use a Pandas call. I also want to remove the big drop in price after Mar, 2014, so I specify the date < 2014-03-01.

google_data = data[data['symbol'] == 'GOOGL']

plt.plot(google_data['date'], google_data['open'])

# remove data > 2014-03-01

google_data_pre_2014 = google_data[ google_data['date'] < pd.to_datetime('2014-03-01')]
plt.plot(google_data_pre_2014['date'], google_data_pre_2014['open'])
plt.xlabel('date')
plt.ylabel('opening price (\$)');

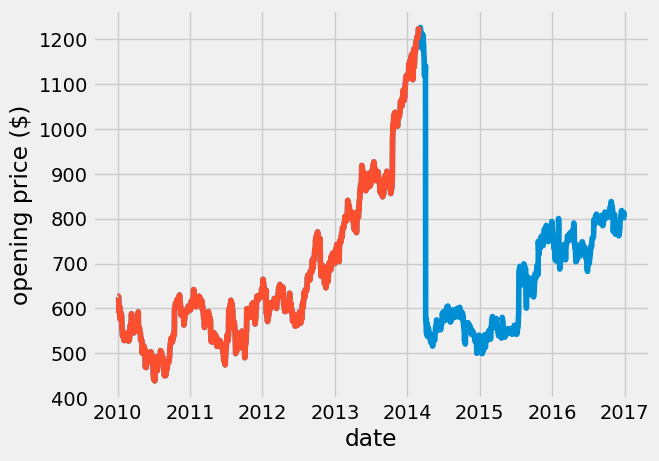
2. Data analysis

The GOOGL stock nearly doubled in price from 2010 through 2014. Day-to-day, the price fluctuates randomly. Here, I look at the fluctuations in price using np.diff.

dprice = np.diff(google_data_pre_2014['open'])
plt.plot(google_data_pre_2014['date'][1:], dprice)
plt.xlabel('date')
plt.ylabel('change in opening price (\$/day)');

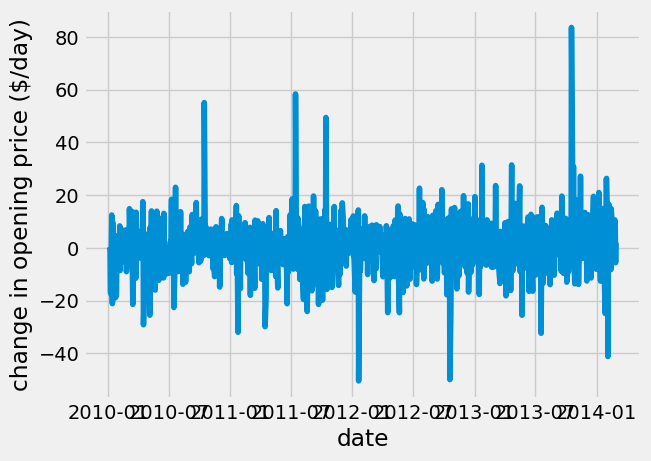
Looking at the price day-to-day, it would appear to be an average change of $0/day. Next, I explore the statistical results of the change in opening price

• mean

• standard deviation

• histogram

mean_dprice = np.mean(dprice)
std_dprice = np.std(dprice)
x = np.linspace(-40, 40)
from scipy import stats
price_pdf = stats.norm.pdf(x, loc = mean_dprice, scale = std_dprice)

plt.hist(dprice, 50, density=True)
plt.plot(x, price_pdf)
plt.title('GOOGL changes in price over 4 years\n'+
         'avg: \${:.2f} stdev: \${:.2f}'.format(mean_dprice, std_dprice));

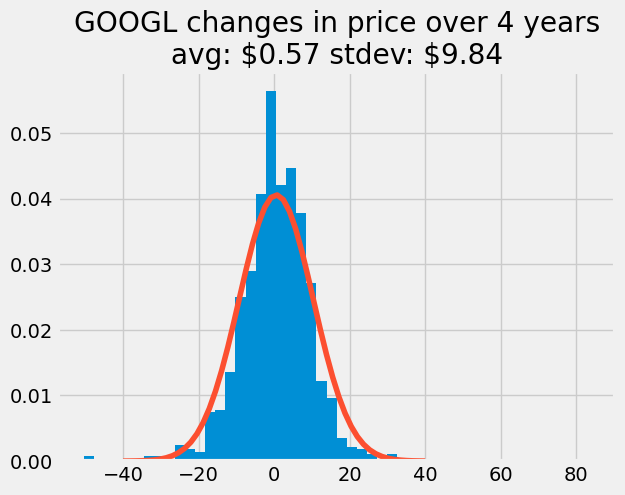
From this statistical result, it looks like the price changes followed a normal distribution with an average change of \(\$0.57\) and a standard deviation of \(\$9.84\).

3. Create random variables

Now, I know the distribution shape and characteristics to simulate the random walk price changes for the GOOGL prices each day. Here, I generate random variables with the following array structure:

Date	model 1	model 2	model 3	…	model N
day 1	\(\Delta \$ model~1\)	\(\Delta \$ model~2\)	\(\Delta \$ model~3\)	…	\(\Delta \$ model~N\)
day 2	\(\Delta \$ model~1\)	\(\Delta \$ model~2\)	\(\Delta \$ model~3\)	…	\(\Delta \$ model~N\)
…	…	…	…	…	…

Each column is one random walk model. Each row is one simulated day. If I want to look at one model predition, I would plot one column. If I want to look at the average result, I take the average of each row. To start, I’ll create 100 random walk models. I use the normal distribution to match the statistical distribution I found in part 2.

rng = default_rng(42)
N_models = 100
dprice_model = rng.normal(size = (len(google_data_pre_2014), N_models), loc = 0.568, scale = 9.838)

plt.hist(dprice, 50, density=True, label = 'NYSE data')
plt.plot(x, price_pdf)
plt.hist(dprice_model[:, 0], 50, density = True, 
         histtype = 'step', 
         linewidth = 3, label = 'model prediction 1')
plt.title('GOOGL changes in price over 4 years\n'+
         'avg: \${:.2f} stdev: \${:.2f}'.format(mean_dprice, std_dprice))
plt.legend();

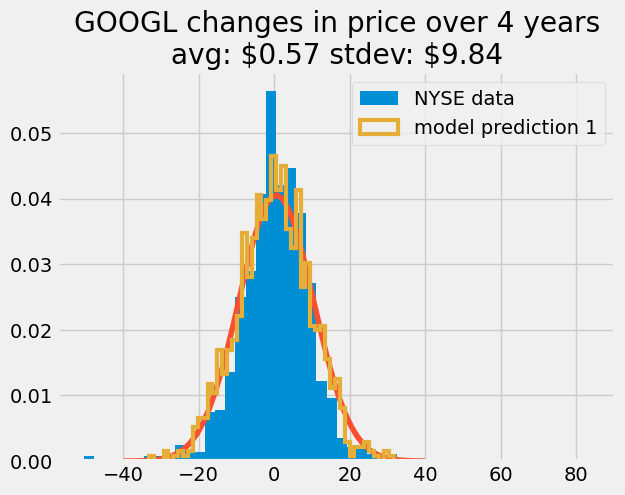
4. Generate random walk predictions

Above, I show tha the simulated data follows the requested normal distribution. Now, I can cumulatively sum these steps to predict the stock prices each day. I use the np.cumsum argument, axis = 0 to sum along the columns i.e. each row becomes the sum of previous rows.

>>> a = np.array([[1,2,3], [4,5,6]])
>>> a
array([[1, 2, 3],
       [4, 5, 6]])
>>>> np.cumsum(a,axis=0)      # sum over rows for each of the 3 columns
array([[1, 2, 3],
       [5, 7, 9]])

Then, I plot all of the random walk models to compare to the NYSE data. The models are given transparency using the alpha = 0.3 command (alpha = 0 is invisible, alpha = 1 is opaque).

price_model = np.cumsum(dprice_model, axis = 0) + google_data_pre_2014['open'].values[0]

plt.plot(google_data_pre_2014['date'], price_model, alpha = 0.3);

plt.plot(google_data_pre_2014['date'], google_data_pre_2014['open'], c = 'k', label = 'NYSE data')
plt.xlabel('date')
plt.ylabel('opening price (\$)');

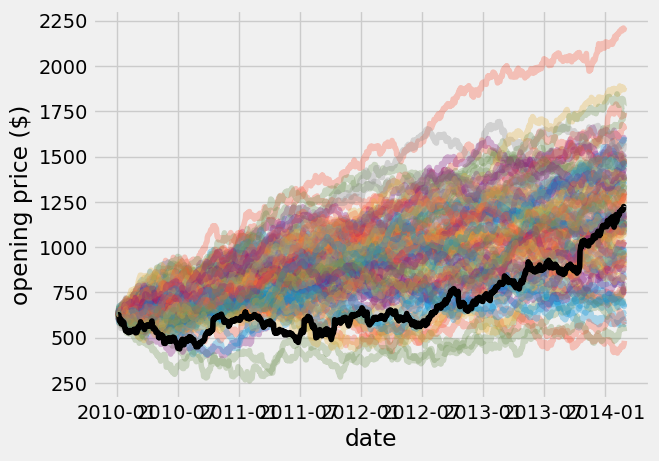
As you would expect, there are a wide variety of predictions for the price of GOOGL stocks using random numbers. Next, I try to get some insight into the average changes in the random walk model. I use the np.mean and np.std across the columns of the price_model prediction data, using axis = 1 now.

price_model_avg = np.mean(price_model, axis = 1)
price_model_std = np.std(price_model, axis = 1)

plt.plot(google_data_pre_2014['date'], price_model, alpha = 0.3);

plt.plot(google_data_pre_2014['date'], google_data_pre_2014['open'], c = 'k', label = 'NYSE data')
plt.xlabel('date')
plt.ylabel('opening price (\$)');

skip = 100
plt.errorbar(google_data_pre_2014['date'][::skip], price_model_avg[::skip],
             yerr = price_model_std[::skip], 
             fmt = 'o',
             c = 'r', 
             label = 'model result', 
            zorder = 3);
plt.legend();
    

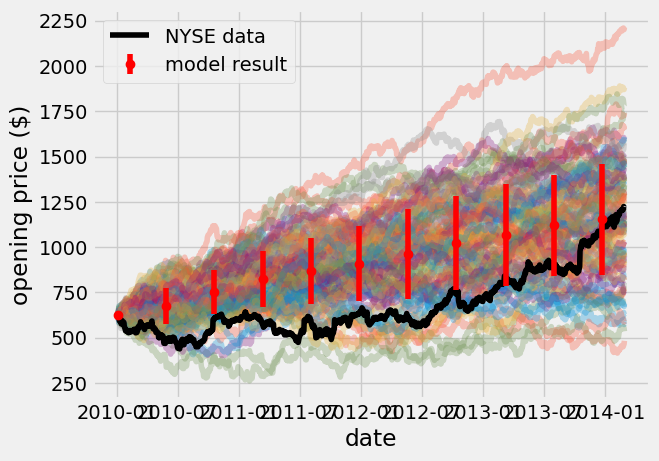
Wrapping up

In this analysis, I went through data exploration, analysis, and Monte Carlo model prediction. The average random walk should resemble a straight line. There are further insights you can get by analyzing the random walk data, but for now it looks like we can accurately predict the growth of GOOGL stock over four years. What are some caveats to this method? If we continue to predict prices into 2015, what would happen compared to the real data?

Next Steps

Now, you can try your hand at predicting stock prices on your own stock. Choose your own stock symbol and go through the same 4 steps I detailed above:

1. Explore data and select your own stock of interest

2. Find statistical description of data: mean and standard deviation _use some of the graphing + analysis techniques in 01_Cheers_stats_beers and 02_Seeing_stats.

3. Create random variables

4. Generate random walk for choose your own stock opening price

Here are the list of stocks in this dataset: ‘A’, ‘AAL’, ‘AAP’, ‘AAPL’, ‘ABBV’, ‘ABC’, ‘ABT’, ‘ACN’, ‘ADBE’, ‘ADI’, ‘ADM’, ‘ADP’, ‘ADS’, ‘ADSK’, ‘AEE’, ‘AEP’, ‘AES’, ‘AET’, ‘AFL’, ‘AGN’, ‘AIG’, ‘AIV’, ‘AIZ’, ‘AJG’, ‘AKAM’, ‘ALB’, ‘ALK’, ‘ALL’, ‘ALLE’, ‘ALXN’, ‘AMAT’, ‘AME’, ‘AMG’, ‘AMGN’, ‘AMP’, ‘AMT’, ‘AMZN’, ‘AN’, ‘ANTM’, ‘AON’, ‘APA’, ‘APC’, ‘APD’, ‘APH’, ‘ARNC’, ‘ATVI’, ‘AVB’, ‘AVGO’, ‘AVY’, ‘AWK’, ‘AXP’, ‘AYI’, ‘AZO’, ‘BA’, ‘BAC’, ‘BAX’, ‘BBBY’, ‘BBT’, ‘BBY’, ‘BCR’, ‘BDX’, ‘BEN’, ‘BHI’, ‘BIIB’, ‘BK’, ‘BLK’, ‘BLL’, ‘BMY’, ‘BSX’, ‘BWA’, ‘BXP’, ‘C’, ‘CA’, ‘CAG’, ‘CAH’, ‘CAT’, ‘CB’, ‘CBG’, ‘CBS’, ‘CCI’, ‘CCL’, ‘CELG’, ‘CERN’, ‘CF’, ‘CFG’, ‘CHD’, ‘CHK’, ‘CHRW’, ‘CHTR’, ‘CI’, ‘CINF’, ‘CL’, ‘CLX’, ‘CMA’, ‘CMCSA’, ‘CME’, ‘CMG’, ‘CMI’, ‘CMS’, ‘CNC’, ‘CNP’, ‘COF’, ‘COG’, ‘COH’, ‘COL’, ‘COO’, ‘COP’, ‘COST’, ‘COTY’, ‘CPB’, ‘CRM’, ‘CSCO’, ‘CSRA’, ‘CSX’, ‘CTAS’, ‘CTL’, ‘CTSH’, ‘CTXS’, ‘CVS’, ‘CVX’, ‘CXO’, ‘D’, ‘DAL’, ‘DD’, ‘DE’, ‘DFS’, ‘DG’, ‘DGX’, ‘DHI’, ‘DHR’, ‘DIS’, ‘DISCA’, ‘DISCK’, ‘DLPH’, ‘DLR’, ‘DLTR’, ‘DNB’, ‘DOV’, ‘DOW’, ‘DPS’, ‘DRI’, ‘DTE’, ‘DUK’, ‘DVA’, ‘DVN’, ‘EA’, ‘EBAY’, ‘ECL’, ‘ED’, ‘EFX’, ‘EIX’, ‘EL’, ‘EMN’, ‘EMR’, ‘ENDP’, ‘EOG’, ‘EQIX’, ‘EQR’, ‘EQT’, ‘ES’, ‘ESRX’, ‘ESS’, ‘ETFC’, ‘ETN’, ‘ETR’, ‘EVHC’, ‘EW’, ‘EXC’, ‘EXPD’, ‘EXPE’, ‘EXR’, ‘F’, ‘FAST’, ‘FB’, ‘FBHS’, ‘FCX’, ‘FDX’, ‘FE’, ‘FFIV’, ‘FIS’, ‘FISV’, ‘FITB’, ‘FL’, ‘FLIR’, ‘FLR’, ‘FLS’, ‘FMC’, ‘FOX’, ‘FOXA’, ‘FRT’, ‘FSLR’, ‘FTI’, ‘FTR’, ‘FTV’, ‘GD’, ‘GE’, ‘GGP’, ‘GILD’, ‘GIS’, ‘GLW’, ‘GM’, ‘GOOG’, ‘GOOGL’, ‘GPC’, ‘GPN’, ‘GPS’, ‘GRMN’, ‘GS’, ‘GT’, ‘GWW’, ‘HAL’, ‘HAR’, ‘HAS’, ‘HBAN’, ‘HBI’, ‘HCA’, ‘HCN’, ‘HCP’, ‘HD’, ‘HES’, ‘HIG’, ‘HOG’, ‘HOLX’, ‘HON’, ‘HP’, ‘HPE’, ‘HPQ’, ‘HRB’, ‘HRL’, ‘HRS’, ‘HSIC’, ‘HST’, ‘HSY’, ‘HUM’, ‘IBM’, ‘ICE’, ‘IDXX’, ‘IFF’, ‘ILMN’, ‘INTC’, ‘INTU’, ‘IP’, ‘IPG’, ‘IR’, ‘IRM’, ‘ISRG’, ‘ITW’, ‘IVZ’, ‘JBHT’, ‘JCI’, ‘JEC’, ‘JNJ’, ‘JNPR’, ‘JPM’, ‘JWN’, ‘K’, ‘KEY’, ‘KHC’, ‘KIM’, ‘KLAC’, ‘KMB’, ‘KMI’, ‘KMX’, ‘KO’, ‘KORS’, ‘KR’, ‘KSS’, ‘KSU’, ‘L’, ‘LB’, ‘LEG’, ‘LEN’, ‘LH’, ‘LKQ’, ‘LLL’, ‘LLTC’, ‘LLY’, ‘LMT’, ‘LNC’, ‘LNT’, ‘LOW’, ‘LRCX’, ‘LUK’, ‘LUV’, ‘LVLT’, ‘LYB’, ‘M’, ‘MA’, ‘MAA’, ‘MAC’, ‘MAR’, ‘MAS’, ‘MAT’, ‘MCD’, ‘MCHP’, ‘MCK’, ‘MCO’, ‘MDLZ’, ‘MDT’, ‘MET’, ‘MHK’, ‘MJN’, ‘MKC’, ‘MLM’, ‘MMC’, ‘MMM’, ‘MNK’, ‘MNST’, ‘MO’, ‘MON’, ‘MOS’, ‘MPC’, ‘MRK’, ‘MRO’, ‘MSFT’, ‘MSI’, ‘MTB’, ‘MTD’, ‘MU’, ‘MUR’, ‘MYL’, ‘NAVI’, ‘NBL’, ‘NDAQ’, ‘NEE’, ‘NEM’, ‘NFLX’, ‘NFX’, ‘NI’, ‘NKE’, ‘NLSN’, ‘NOC’, ‘NOV’, ‘NRG’, ‘NSC’, ‘NTAP’, ‘NTRS’, ‘NUE’, ‘NVDA’, ‘NWL’, ‘NWS’, ‘NWSA’, ‘O’, ‘OKE’, ‘OMC’, ‘ORCL’, ‘ORLY’, ‘OXY’, ‘PAYX’, ‘PBCT’, ‘PBI’, ‘PCAR’, ‘PCG’, ‘PCLN’, ‘PDCO’, ‘PEG’, ‘PEP’, ‘PFE’, ‘PFG’, ‘PG’, ‘PGR’, ‘PH’, ‘PHM’, ‘PKI’, ‘PLD’, ‘PM’, ‘PNC’, ‘PNR’, ‘PNW’, ‘PPG’, ‘PPL’, ‘PRGO’, ‘PRU’, ‘PSA’, ‘PSX’, ‘PVH’, ‘PWR’, ‘PX’, ‘PXD’, ‘PYPL’, ‘QCOM’, ‘QRVO’, ‘R’, ‘RAI’, ‘RCL’, ‘REGN’, ‘RF’, ‘RHI’, ‘RHT’, ‘RIG’, ‘RL’, ‘ROK’, ‘ROP’, ‘ROST’, ‘RRC’, ‘RSG’, ‘RTN’, ‘SBUX’, ‘SCG’, ‘SCHW’, ‘SE’, ‘SEE’, ‘SHW’, ‘SIG’, ‘SJM’, ‘SLB’, ‘SLG’, ‘SNA’, ‘SNI’, ‘SO’, ‘SPG’, ‘SPGI’, ‘SPLS’, ‘SRCL’, ‘SRE’, ‘STI’, ‘STT’, ‘STX’, ‘STZ’, ‘SWK’, ‘SWKS’, ‘SWN’, ‘SYF’, ‘SYK’, ‘SYMC’, ‘SYY’, ‘T’, ‘TAP’, ‘TDC’, ‘TDG’, ‘TEL’, ‘TGNA’, ‘TGT’, ‘TIF’, ‘TJX’, ‘TMK’, ‘TMO’, ‘TRIP’, ‘TROW’, ‘TRV’, ‘TSCO’, ‘TSN’, ‘TSO’, ‘TSS’, ‘TWX’, ‘TXN’, ‘TXT’, ‘UAA’, ‘UAL’, ‘UDR’, ‘UHS’, ‘ULTA’, ‘UNH’, ‘UNM’, ‘UNP’, ‘UPS’, ‘URBN’, ‘URI’, ‘USB’, ‘UTX’, ‘V’, ‘VAR’, ‘VFC’, ‘VIAB’, ‘VLO’, ‘VMC’, ‘VNO’, ‘VRSK’, ‘VRSN’, ‘VRTX’, ‘VTR’, ‘VZ’, ‘WAT’, ‘WBA’, ‘WDC’, ‘WEC’, ‘WFC’, ‘WFM’, ‘WHR’, ‘WLTW’, ‘WM’, ‘WMB’, ‘WMT’, ‘WRK’, ‘WU’, ‘WY’, ‘WYN’, ‘WYNN’, ‘XEC’, ‘XEL’, ‘XL’, ‘XLNX’, ‘XOM’, ‘XRAY’, ‘XRX’, ‘XYL’, ‘YHOO’, ‘YUM’, ‘ZBH’, ‘ZION’, ‘ZTS’