import numpy as np
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')

from numpy.random import default_rng
rng = default_rng()

HW_04 - Exercise: failure prediction

In the dropping keys experiment, we ended the trials when the virtual person succeeded in entering the room. What would this look like if an engineering process failed when a certain device is used?

Consider a manufacturing plant that produces uses O-rings in the assembly. The O-rings are the weakest link in the design. Your company needs to use 10 O-rings in every device you manufacture. If one O-ring fails, the whole device fails. Your quality control team knows the O-rings fail 1-out-of-10 times. When you test a device, if it fails the rings are discarded and ten more used to assemble the device.

Your manager wants you to come up with a process to assemble these parts. The manager thinks that each part will need to be reassembled 10% of the time, regardless of the number of times its failed. See if you can recommend a process that makes use of this new knowledge that repeated assemblies have a decreased chance of failure.

N = 10000
cases = np.zeros(N)
keys = np.arange(10)
for ncase in range(N):
    tries = 0
    key = 10
    while key != 0:
        key = rng.integers(len(keys), size = 1)
        tries += 1
    cases[ncase] = tries
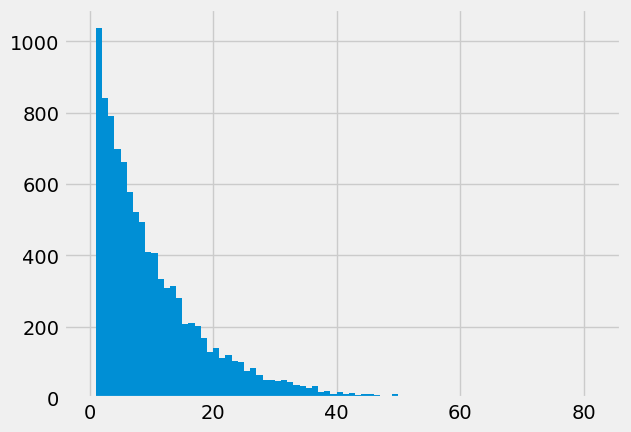
plt.hist(cases, bins = np.arange(np.max(cases)))

(array([  0., 947., 895., 831., 737., 695., 573., 519., 506., 426., 414.,
        336., 319., 272., 233., 232., 192., 196., 168., 155., 137., 117.,
        111.,  90.,  69.,  78.,  80.,  71.,  67.,  56.,  42.,  44.,  37.,
         26.,  31.,  26.,  23.,  25.,  20.,  15.,  18.,  11.,  14.,  20.,
          9.,  11.,   5.,   5.,  10.,  13.,  11.,   8.,   7.,   7.,   6.,
          6.,   1.,   0.,   2.,   3.,   1.,   0.,   3.,   1.,   0.,   2.,
          0.,   0.,   1.,   5.,   2.,   1.,   1.,   1.,   0.,   0.,   0.,
          0.,   0.,   0.,   0.,   0.,   0.,   0.,   0.,   1.,   0.,   0.,
          0.,   0.,   0.,   1.,   0.,   0.,   0.,   1.,   0.,   0.,   0.,
          0.,   0.]),
 array([  0.,   1.,   2.,   3.,   4.,   5.,   6.,   7.,   8.,   9.,  10.,
         11.,  12.,  13.,  14.,  15.,  16.,  17.,  18.,  19.,  20.,  21.,
         22.,  23.,  24.,  25.,  26.,  27.,  28.,  29.,  30.,  31.,  32.,
         33.,  34.,  35.,  36.,  37.,  38.,  39.,  40.,  41.,  42.,  43.,
         44.,  45.,  46.,  47.,  48.,  49.,  50.,  51.,  52.,  53.,  54.,
         55.,  56.,  57.,  58.,  59.,  60.,  61.,  62.,  63.,  64.,  65.,
         66.,  67.,  68.,  69.,  70.,  71.,  72.,  73.,  74.,  75.,  76.,
         77.,  78.,  79.,  80.,  81.,  82.,  83.,  84.,  85.,  86.,  87.,
         88.,  89.,  90.,  91.,  92.,  93.,  94.,  95.,  96.,  97.,  98.,
         99., 100., 101.]),
 <BarContainer object of 101 artists>)

try_01 = np.sum(cases == 1)/N
try_02 = np.sum(cases == 2)/N
try_03 = np.sum(cases == 3)/N
try_04 = np.sum(cases == 4)/N

print('failure on try 1: {}, {:1.2f}%'.format(try_01*N, 100*try_01))

print('failure on try 2: {}, {:1.2f}%'.format(try_02*N, 100*try_02))

print('failure on try 3: {}, {:1.2f}%'.format(try_03*N, 100*try_03))

print('failure on try 4: {}, {:1.2f}%'.format(try_04*N, 100*try_04))

failure on try 1: 947.0000000000001, 9.47%
failure on try 2: 895.0, 8.95%
failure on try 3: 830.9999999999999, 8.31%
failure on try 4: 737.0, 7.37%

1/10*9/10*9/10*9/10

0.07289999999999999