What is the fastest path between two points?

We want to design a track that minimizes the time it takes to descend from height, $h$, to height 0 and we want to travel forward by distance, $L$.

What shape should the track take?

total time is, $T$,

$$T = \int_0^L\frac{ds}{v}$$

For a first approximation, consider sliding without friction,

$$mgh = \frac{1}{2}mv^2 + mgf(x)$$

Our track can only have 1 height, $y$ for every position, $x$, so

$$y(x) = f(x)$$

and

$$v = \sqrt{2g(h-f(x))}$$

and the distance traveled is $ds = \sqrt{dx^2+dy^2}= \sqrt{dx^2+dx^2\frac{df}{dx}^2}$ or

$$ds = dx\sqrt{1+f'^2}$$

our total time, $T$, is now

$$T = \int_0^L\frac{ds}{v}=\int_0^L\sqrt{\frac{1+f'^2}{2g(h-f)}}dx$$

begin
using Plots
using LaTeXStrings
end

g = 9.81

9.81

F(f, df, h = 1) = ((1+df^2)/(2*g*(h-f))).^0.5

F (generic function with 2 methods)

function T(F, f, df, L = 1, dx=0.0001)
    x = range(dx, L, step = dx)
    val = F.(f.(x), df.(x)).*dx
    T = sum(val)
    return T
end

T (generic function with 3 methods)

function build_parabola(p1, h=1, L=1)
    x1, y1 = p1
    A = [0 0 1; 
         x1^2 x1 x1^0;
         L^2 L L^0]
    b = [h, y1, 0]
    C = A\b
    f(x) = C[1]*x^2+C[2]*x+C[3]
    df(x) = 2*C[1]*x +C[2]
    return f, df
end

build_parabola (generic function with 3 methods)

begin
    y1s = range(0, 0.7, step=0.05)
    T_array = zeros(length(y1s))
    P = plot([0, 1], [1, 0], 
             markershape=:rect, 
             linetype=:scatter,
            label = "start-stop")
    dx = 0.0001
    x = range(dx, 1, step = dx)
    for (i, y1) in enumerate(y1s)
        f, df = build_parabola([0.5, y1])
        T_array[i] = T(F, f, df, 1, dx)
        plot!(P, x, f.(x), label = "y"*string(i))
    end
plot!(P, title = "Varying paths from start to stop",
     xlabel = "X-location (m)",
     ylabel = "Y-location (m)")
plot!(ones(length(y1s)).*0.5, 
      y1s, 
      markershape=:circ,
      linetype=:scatter,
     label = "fixed points")
    P
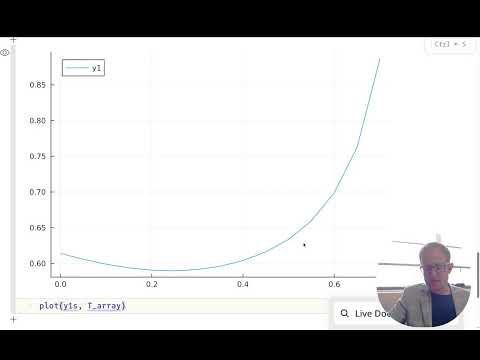
end

plot(y1s, T_array, 
     title = "Optimizing fastest path",
    xlabel = L"Y-position fixed at $x=\frac{L}{2}$",
    ylabel = "Total time to bottom (s)")

Built with Julia 1.12.4 and

LaTeXStrings 1.4.0
Plots 1.40.20

Dynamics

What is the fastest path between two points?