Principle of Least Action and Lagrangian Mechanics

Introduction to the Topic

This video explores the foundational concept of the principle of least action and its mathematical formulation through the Lagrangean approach to classical mechanics. The core idea is that physical systems naturally follow paths that minimize a quantity called the action. This principle underpins the equations of motion for objects subject to forces like gravity and springs.

The Action Principle and Variations

The Lagrangian \(L\) is defined as the difference between kinetic energy \(T\) and potential energy \(V\) (i.e., \(L = T - V\)). The Action \(S\) is the time integral of the Lagrangian. The principle of least action states that the true path of a system (such as the motion of a particle) is the one that minimizes this integral —the **action functional—between two moments in time.

Mathematically, this is expressed as:

\(\int_{t_1}^{t_2} L(t) \, dt\)

being minimized among all possible paths between the initial and final states. To formalize this, we consider small variations (or "deviations") from the true path and set the first variation of the action to zero. This leads to a system of Euler-Lagrange equations, which are differential equations describing the motion of the system.

Derivation and Key Steps

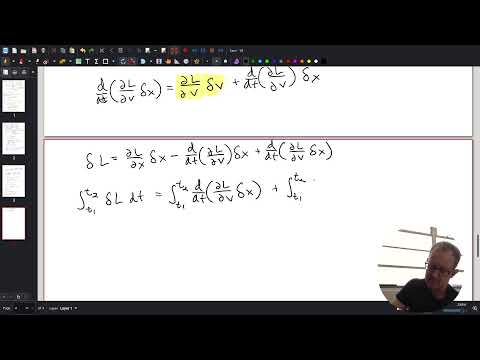
The derivation involves calculus of variations and integration by parts. Starting from the variation of the action:

\(\delta S = \int_{t_1}^{t_2} \delta L \, dt\)

we expand the change in the Lagrangian \(\delta L\) using the chain rule. This results in terms involving changes in position (\(\delta x\)) and velocity (\(\delta v\)). By integrating by parts one of these terms, we separate the contributions into boundary terms and bulk terms.

Crucially, the bulk terms (those not evaluated at the endpoints in time) must vanish for the variation to be stationary. This process separates variables, allowing us to write a Lagrange equation where the derivative of one term (related to velocity) minus another term (related to position) equals zero.

The final key equation obtained is: \(\frac{d}{dt}\left( \frac{\partial L}{\partial \dot{q}} \right) - \frac{\partial L}{\partial q} = 0\) For a simple case where \(L = T - V\) depends on position \(q\) and velocity \(\dot{q}\), this yields a second-order ordinary differential equation describing the motion of a system.

Connection to Kinetic and Potential Energy

The Lagrangian naturally incorporates kinetic energy, which depends on both position and velocity, and potential energy, which depends only on position (though the formalism allows for more general forms). The separation of these terms reflects the conservation of energy in the absence of external forces (like friction).

The method implicitly requires boundary conditions at the start and end times (\(t_1 \)and \(t_2\)), such as the initial and final positions and velocities. This is distinct from boundary conditions in space (like fixed endpoints), but the principle still selects the physically meaningful path.

The Role of the Euler-Lagrange Equation

The resulting differential equation is nonlinear in general, but for many simple systems (e.g., a particle in a conservative force field), it becomes a second-order ordinary differential equation. This equation uniquely determines the motion of the system once the Lagrangian is specified and the boundary conditions are set.

A classic example is the harmonic oscillator or a pendulum, where the Lagrangian leads to the simple harmonic motion equation. More complex curves like cycloids or catenary shapes also emerge as solutions when the Lagrangian corresponds to specific physical systems (e.g., a mass sliding under constant acceleration).

Interpretation and Physical Meaning

The principle of least action is a statement that nature minimizes the action along its actual path. This is analogous to how a beam bends to minimize its length (the straight line) or a light ray travels the shortest path through a medium. In mechanics, the "shortest path" in configuration space is not always the straight line, but the path that balances kinetic and potential energies over time.

The method requires no external work (except possibly through boundary conditions), meaning energy is conserved between kinetic and potential forms. The integration by parts step highlights the trade-off between changes in velocity and position along the path.

Relation to Other Mathematical Tricks

While the derivation in the video took a long route, there is a mathematical identity (like the calculus of variations) that simplifies finding the "shortest path" (geodesic) or minimal action curve. For example, in many cases, the shortest path between two points under a conservative force is a straight line in velocity-space or a curve of constant curvature, such as a cycloid or catenary. The Lagrangian method encapsulates these insights in a general framework.

Wrapping Up

In summary, the video explains how the principle of least action is formulated mathematically using the Lagrangian formalism. By expressing the action in terms of the systems kinetic and potential energy, and applying calculus of variations, we derive second-order differential equations that govern the motion of mechanical systems. This approach provides a powerful and elegant way to connect energy considerations with the equations of motion. The key takeaway is that the path taken by a physical system is not just any path, but the one that makes the action functional stationary—thereby balancing the system's energy in the most efficient way possible.