Newton's Laws vs. Lagrangian Mechanics: A Comparative Analysis
Understanding the Problem
The problem involves comparing two approaches in classical mechanics:
Newtonian Mechanics: Focusing on forces, accelerations, and inertial frames.
Lagrangian Mechanics: Emphasizing energy principles (kinetic and potential) and constraints.
Newtonian Approach
Newton's laws of motion are applied to analyze mechanical systems.
Forces acting on a system determine the equations of motion.
Appropriate for complex force analysis but can be cumbersome for certain problems.
Lagrangian Approach
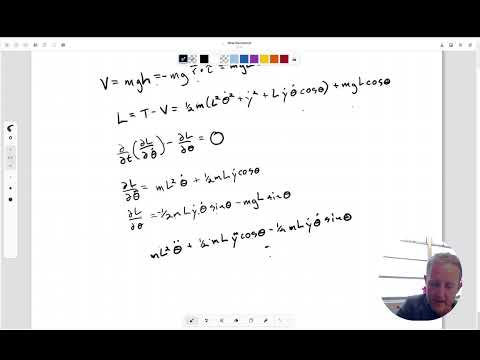
Uses Lagrangian function \(L = T - V\) where \(T\) is kinetic energy and \(V\) is potential energy.
Constraints are incorporated to simplify equations of motion.
Suitable for systems with holonomic constraints (e.g., pendulums, rolling without slipping).
Example: Pendulum Analysis
Newtonian Perspective
Identify forces:
Gravitational force (\(mg\)) acting downward.
Normal force balancing the perpendicular component of gravity.
Tension in the string providing centripetal force.
Resolve forces into radial and tangential components to derive equations of motion.
Euler's laws or Newton's second law for rotational motion are applied:
\(m l \ddot{\theta} = -mg \sin\theta\)
Simplified for small angles: \(\ddot{\theta} + \frac{g}{l}\theta = 0\)
Lagrangian Perspective
Define kinetic energy (\(T\)) and potential energy (\(V\)):
\(T = \frac{1}{2} m v^2\)
\(V = mgl(1 - \cos\theta)\)
Formulate the Lagrangian function:
\(L = T - V\)
Apply Euler-Lagrange equation for generalized coordinate \(\theta\):
\(\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta}}\right) - \frac{\partial L}{\partial \theta} = 0\)
Results in the same equation of motion: \(m l \ddot{\theta} + mg \sin\theta = 0\)
Advantages of Lagrangian Mechanics
Systematic approach to derive equations of motion.
Incorporates constraints naturally, reducing complexity.
Suitable for multi-degree-of-freedom systems.
Conclusion
While both approaches yield the same results, the Lagrangian method offers a more streamlined and generalized framework for complex mechanical systems compared to Newtonian mechanics.